Mid-unit Review Multiply Using Foil or by the Front Term

Prerequisites

Polynomials

Learning Objectives

In this section students will:

Place the degree and leading coefficient of polynomials.
Add and decrease polynomials.
Multiply polynomials.
Use FOIL to multiply binomials.
Perform operations with polynomials of several variables.

Earl is edifice a doghouse, whose front is in the shape of a square topped with a triangle. There will exist a rectangular door through which the domestic dog can enter and leave the house. Earl wants to discover the area of the front of the doghouse and then that he tin buy the correct amount of paint. Using the measurements of the front of the business firm, shown in (Figure), nosotros tin can create an expression that combines several variable terms, allowing us to solve this trouble and others like information technology.

Sketch of a house formed by a square and a triangle based on the top of the square. A rectangle is placed at the bottom center of the square to mark a doorway. The height of the door is labeled: x and the width of the door is labeled: 1 foot. The side of the square is labeled: 2x. The height of the triangle is labeled: 3/2 feet. — **Figure 1.**

First find the expanse of the foursquare in square feet.

$\begin{array}{ccc}\hfill A& =& {s}^{2}\hfill \\ & =& {\left(2x\right)}^{2}\hfill \\ & =& 4{x}^{2}\hfill \end{array}$

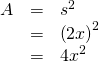
Then find the area of the triangle in square feet.

$\begin{array}{ccc}\hfill A& =& \frac{1}{2}bh\hfill \\ & =& \text{ }\frac{1}{2}\left(2x\right)\left(\frac{3}{2}\right)\hfill \\ & =& \text{ }\frac{3}{2}x\hfill \end{array}$

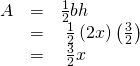
Adjacent find the expanse of the rectangular door in square feet.

$\begin{array}{ccc}\hfill A& =& lw\hfill \\ & =& x\cdot 1\hfill \\ \hfill & =& x\hfill \end{array}$

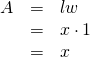
The area of the front of the doghouse can be found by calculation the areas of the square and the triangle, and and then subtracting the surface area of the rectangle. When nosotros do this, we get $\,4{x}^{2}+\frac{3}{2}x-x\,{\text{ft}}^{2},$ or $\,4{x}^{2}+\frac{1}{2}x\,$ ft².

In this department, nosotros will examine expressions such as this one, which combine several variable terms.

Identifying the Degree and Leading Coefficient of Polynomials

The formula just institute is an example of a polynomial, which is a sum of or difference of terms, each consisting of a variable raised to a nonnegative integer power. A number multiplied by a variable raised to an exponent, such every bit $\,384\pi ,$ is known as a coefficient. Coefficients can be positive, negative, or aught, and tin can be whole numbers, decimals, or fractions. Each product $\,{a}_{i}{x}^{i},$ such equally $\,384\pi w,$ is a term of a polynomial. If a term does not contain a variable, it is chosen a constant.

A polynomial containing only i term, such as $\,5{x}^{4},$ is called a monomial. A polynomial containing two terms, such as $\,2x-9,$ is called a binomial. A polynomial containing three terms, such as $\,-3{x}^{2}+8x-7,$ is called a trinomial.

We can find the degree of a polynomial by identifying the highest power of the variable that occurs in the polynomial. The term with the highest caste is called the leading term because it is normally written first. The coefficient of the leading term is called the leading coefficient. When a polynomial is written then that the powers are descending, we say that it is in standard form.

A polynomial reading: a sub n times x to the nth power plus and so on plus a sub 2 times x squared plus a sub one times x plus a subzero is shown. The a in the term a sub n is labeled: leading coefficient. The n in the term x to the nth power is labeled: degree. Finally, the entire term is labeled as: Leading term.

Polynomials

A polynomial is an expression that can be written in the class

${a}_{n}{x}^{n}+...+{a}_{2}{x}^{2}+{a}_{1}x+{a}_{0}$

Each real number a_i is called a coefficient. The number $\,{a}_{0}\,$ that is non multiplied by a variable is chosen a constant. Each product $\,{a}_{i}{x}^{i}\,$ is a term of a polynomial. The highest power of the variable that occurs in the polynomial is chosen the caste of a polynomial. The leading term is the term with the highest power, and its coefficient is called the leading coefficient.

How To

Given a polynomial expression, identify the caste and leading coefficient.

Observe the highest power of x to determine the caste.
Identify the term containing the highest ability of x to discover the leading term.
Identify the coefficient of the leading term.

Attempt Information technology

Identify the degree, leading term, and leading coefficient of the polynomial $\,4{x}^{2}-{x}^{6}+2x-6.$

[reveal-answer q="fs-id1167339196860″]Show Solution[/reveal-reply]
[subconscious-answer a="fs-id1167339196860″]

The degree is half-dozen, the leading term is $\,-{x}^{6},$ and the leading coefficient is $\,-1.$

[/subconscious-answer]

Adding and Subtracting Polynomials

We tin can add and decrease polynomials past combining like terms, which are terms that comprise the same variables raised to the same exponents. For example, $\,5{x}^{2}\,$ and $\,-2{x}^{2}\,$ are like terms, and tin exist added to get $\,3{x}^{2},$ but $\,3x\,$ and $\,3{x}^{2}\,$ are not similar terms, and therefore cannot be added.

How To

Given multiple polynomials, add or subtract them to simplify the expressions.

Combine like terms.
Simplify and write in standard form.

Adding Polynomials

Find the sum.

$\left(12{x}^{2}+9x-21\right)+\left(4{x}^{3}+8{x}^{2}-5x+20\right)$

[reveal-reply q="fs-id1167339300037″]Show Solution[/reveal-respond]
[hidden-answer a="fs-id1167339300037″]

$\begin{array}{cc}4{x}^{3}+\left(12{x}^{2}+8{x}^{2}\right)+\left(9x-5x\right)+\left(-21+20\right) \hfill & \phantom{\rule{2em}{0ex}}\text{ }\text{Combine like terms}.\hfill \\ 4{x}^{3}+20{x}^{2}+4x-1\hfill & \phantom{\rule{2em}{0ex}}\text{ }\text{Simplify}.\hfill \end{array}$

[/subconscious-answer]

Analysis

We can cheque our answers to these types of problems using a graphing reckoner. To bank check, graph the trouble every bit given along with the simplified reply. The two graphs should exist equivalent. Be certain to utilise the same window to compare the graphs. Using dissimilar windows can make the expressions seem equivalent when they are non.

Try Information technology

Find the sum.

$\left(2{x}^{3}+5{x}^{2}-x+1\right)+\left(2{x}^{2}-3x-4\right)$

[reveal-answer q="fs-id1167339223528″]Evidence Solution[/reveal-answer]
[subconscious-answer a="fs-id1167339223528″]

$2{x}^{3}+7{x}^{2}-4x-3$

[/hidden-answer]

Subtracting Polynomials

Find the difference.

$\left(7{x}^{4}-{x}^{2}+6x+1\right)-\left(5{x}^{3}-2{x}^{2}+3x+2\right)$

[reveal-answer q="fs-id1167339158579″]Show Solution[/reveal-respond]
[subconscious-respond a="fs-id1167339158579″]

$\begin{array}{cc}7{x}^{4}-5{x}^{3}+\left(-{x}^{2}+2{x}^{2}\right)+\left(6x-3x\right)+\left(1-2\right)\text{ }\hfill & \phantom{\rule{1em}{0ex}}\text{Combine like terms}.\hfill \\ 7{x}^{4}-5{x}^{3}+{x}^{2}+3x-1\hfill & \phantom{\rule{1em}{0ex}}\text{Simplify}.\hfill \end{array}$

[/hidden-answer]

Analysis

Note that finding the difference between two polynomials is the aforementioned every bit calculation the opposite of the second polynomial to the get-go.

Effort It

Detect the difference.

$\left(-7{x}^{3}-7{x}^{2}+6x-2\right)-\left(4{x}^{3}-6{x}^{2}-x+7\right)$

[reveal-answer q="fs-id1167339260393″]Bear witness Solution[/reveal-answer]
[subconscious-answer a="fs-id1167339260393″]

$-11{x}^{3}-{x}^{2}+7x-9$

[/hidden-answer]

Multiplying Polynomials

Multiplying polynomials is a bit more challenging than calculation and subtracting polynomials. We must use the distributive holding to multiply each term in the first polynomial by each term in the 2d polynomial. Nosotros then combine like terms. We tin can also use a shortcut chosen the FOIL method when multiplying binomials. Sure special products follow patterns that we tin can memorize and use instead of multiplying the polynomials by hand each fourth dimension. Nosotros volition look at a multifariousness of means to multiply polynomials.

Multiplying Polynomials Using the Distributive Belongings

To multiply a number by a polynomial, we use the distributive holding. The number must be distributed to each term of the polynomial. We tin distribute the $\,2\,$ in $\,2\left(x+7\right)\,$ to obtain the equivalent expression $\,2x+14.\,$ When multiplying polynomials, the distributive property allows usa to multiply each term of the first polynomial past each term of the second. Nosotros then add the products together and combine like terms to simplify.

How To

Given the multiplication of two polynomials, use the distributive holding to simplify the expression.

Multiply each term of the first polynomial by each term of the second.
Combine like terms.
Simplify.

Multiplying Polynomials Using the Distributive Property

Find the product.

$\left(2x+1\right)\left(3{x}^{2}-x+4\right)$

[reveal-answer q="fs-id1167339306275″]Show Solution[/reveal-answer]
[hidden-answer a="fs-id1167339306275″]

$\begin{array}{cc}2x\left(3{x}^{2}-x+4\right)+1\left(3{x}^{2}-x+4\right) \hfill & \phantom{\rule{2em}{0ex}}\text{ }\text{Use the distributive property}.\hfill \\ \left(6{x}^{3}-2{x}^{2}+8x\right)+\left(3{x}^{2}-x+4\right)\hfill & \phantom{\rule{2em}{0ex}}\text{ }\text{Multiply}.\hfill \\ 6{x}^{3}+\left(-2{x}^{2}+3{x}^{2}\right)+\left(8x-x\right)+4\hfill & \phantom{\rule{2em}{0ex}}\text{ }\text{Combine like terms}.\hfill \\ 6{x}^{3}+{x}^{2}+7x+4 \hfill & \phantom{\rule{2em}{0ex}}\text{ }\text{Simplify}.\hfill \end{array}$

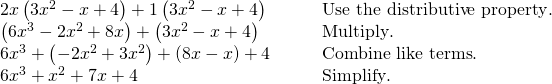
[/hidden-respond]

Endeavor It

Find the production.

$\left(3x+2\right)\left({x}^{3}-4{x}^{2}+7\right)$

[reveal-respond q="fs-id1167339223342″]Show Solution[/reveal-answer]
[hidden-answer a="fs-id1167339223342″]

$3{x}^{4}-10{x}^{3}-8{x}^{2}+21x+14$

[/hidden-reply]

Using FOIL to Multiply Binomials

A shortcut called FOIL is sometimes used to discover the product of two binomials. It is called FOIL because nosotros multiply the first terms, the outer terms, the inner terms, then the fiftyast terms of each binomial.

Two quantities in parentheses are being multiplied, the first being: a times x plus b and the second being: c times x plus d. This expression equals ac times x squared plus ad times x plus bc times x plus bd. The terms ax and cx are labeled: First Terms. The terms ax and d are labeled: Outer Terms. The terms b and cx are labeled: Inner Terms. The terms b and d are labeled: Last Terms.

The FOIL method arises out of the distributive property. Nosotros are just multiplying each term of the first binomial past each term of the second binomial, and then combining like terms.

How To

Given two binomials, use FOIL to simplify the expression.

Multiply the first terms of each binomial.
Multiply the outer terms of the binomials.
Multiply the inner terms of the binomials.
Multiply the last terms of each binomial.
Add the products.
Combine like terms and simplify.

Using FOIL to Multiply Binomials

Use FOIL to find the production.

$\left(2x-18\right)\left(3x+3\right)$

[reveal-reply q="394130″]Evidence Solution[/reveal-respond]
[hidden-answer a="394130″]

Find the product of the commencement terms.

Detect the product of the outer terms.

Find the product of the inner terms.

Find the product of the last terms.

$\begin{array}{cc}6{x}^{2}+6x-54x-54\hfill & \phantom{\rule{2em}{0ex}}\text{Add the products}.\hfill \\ 6{x}^{2}+\left(6x-54x\right)-54\hfill & \phantom{\rule{2em}{0ex}}\text{Combine like terms}.\hfill \\ 6{x}^{2}-48x-54\hfill & \phantom{\rule{2em}{0ex}}\text{Simplify}.\hfill \end{array}$

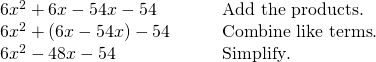
[/hidden-answer]

Try It

Employ FOIL to find the product.

$\left(x+7\right)\left(3x-5\right)$

[reveal-reply q="fs-id1167339216120″]Show Solution[/reveal-answer]
[hidden-answer a="fs-id1167339216120″]

$3{x}^{2}+16x-35$

[/hidden-respond]

Perfect Square Trinomials

Certain binomial products have special forms. When a binomial is squared, the result is called a perfect square trinomial. We tin can find the square past multiplying the binomial past itself. Nonetheless, there is a special form that each of these perfect square trinomials takes, and memorizing the form makes squaring binomials much easier and faster. Allow'due south look at a few perfect square trinomials to familiarize ourselves with the form.

$\begin{array}{ccc}\hfill \text{ }{\left(x+5\right)}^{2}& =& {x}^{2}+10x+25\hfill \\ \hfill {\left(x-3\right)}^{2}& =& \text{ }{x}^{2}-6x+9\hfill \\ \hfill {\left(4x-1\right)}^{2}& =& 16{x}^{2}-8x+1\hfill \end{array}$

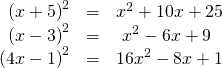
Notice that the first term of each trinomial is the square of the first term of the binomial and, similarly, the last term of each trinomial is the foursquare of the final term of the binomial. The center term is double the production of the ii terms. Lastly, we see that the first sign of the trinomial is the aforementioned as the sign of the binomial.

Perfect Square Trinomials

When a binomial is squared, the result is the first term squared added to double the production of both terms and the concluding term squared.

${\left(x+a\right)}^{2}=\left(x+a\right)\left(x+a\right)={x}^{2}+2ax+{a}^{2}$

How To

Given a binomial, foursquare it using the formula for perfect square trinomials.

Foursquare the commencement term of the binomial.
Square the last term of the binomial.
For the middle term of the trinomial, double the product of the two terms.
Add together and simplify.

Expanding Perfect Squares

Expand $\,{\left(3x-8\right)}^{2}.$

[reveal-answer q="fs-id1167339428957″]Show Solution[/reveal-respond]
[subconscious-answer a="fs-id1167339428957″]

Brainstorm past squaring the first term and the last term. For the eye term of the trinomial, double the production of the two terms.

${\left(3x\right)}^{2}-2\left(3x\right)\left(8\right)+{\left(-8\right)}^{2}$ [/hidden-answer]

Simplify

$\,9{x}^{2}-48x+64.$

Try It

Aggrandize $\,{\left(4x-1\right)}^{2}.$

[reveal-answer q="fs-id1167339176899″]Show Solution[/reveal-respond]
[hidden-answer a="fs-id1167339176899″]

$16{x}^{2}-8x+1$

[/hidden-answer]

Difference of Squares

Another special product is chosen the difference of squares, which occurs when we multiply a binomial by another binomial with the aforementioned terms but the opposite sign. Let's see what happens when we multiply $\,\left(x+1\right)\left(x-1\right)\,$ using the FOIL method.

$\begin{array}{ccc}\hfill \left(x+1\right)\left(x-1\right)& =& {x}^{2}-x+x-1\hfill \\ & =& {x}^{2}-1\hfill \end{array}$

The middle term drops out, resulting in a departure of squares. Just every bit nosotros did with the perfect squares, permit's expect at a few examples.

$\begin{array}{ccc}\hfill \left(x+5\right)\left(x-5\right)& =& {x}^{2}-25\hfill \\ \hfill \left(x+11\right)\left(x-11\right)& =& {x}^{2}-121\hfill \\ \hfill \left(2x+3\right)\left(2x-3\right)& =& 4{x}^{2}-9\hfill \end{array}$

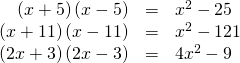
Because the sign changes in the 2nd binomial, the outer and inner terms cancel each other out, and we are left only with the square of the commencement term minus the foursquare of the last term.

Is at that place a special course for the sum of squares?

No. The divergence of squares occurs because the opposite signs of the binomials crusade the center terms to disappear. There are no 2 binomials that multiply to equal a sum of squares.

Difference of Squares

When a binomial is multiplied by a binomial with the same terms separated by the contrary sign, the upshot is the square of the get-go term minus the foursquare of the concluding term.

$\left(a+b\right)\left(a-b\right)={a}^{2}-{b}^{2}$

How To

Given a binomial multiplied past a binomial with the same terms but the opposite sign, find the deviation of squares.

Square the outset term of the binomials.
Foursquare the last term of the binomials.
Subtract the foursquare of the last term from the square of the kickoff term.

Multiplying Binomials Resulting in a Divergence of Squares

Multiply $\,\left(9x+4\right)\left(9x-4\right).$

[reveal-reply q="fs-id1167339273948″]Show Solution[/reveal-respond]
[hidden-reply a="fs-id1167339273948″]

Foursquare the first term to become $\,{\left(9x\right)}^{2}=81{x}^{2}.\,$ Square the last term to go $\,{4}^{2}=16.\,$ Decrease the square of the last term from the square of the starting time term to discover the product of $\,81{x}^{2}-16.$

[/hidden-respond]

Endeavor Information technology

Multiply $\,\left(2x+7\right)\left(2x-7\right).$

[reveal-answer q="fs-id1167339318295″]Show Solution[/reveal-respond]
[hidden-answer a="fs-id1167339318295″]

$4{x}^{2}-49$

[/hidden-answer]

Performing Operations with Polynomials of Several Variables

We have looked at polynomials containing only i variable. Notwithstanding, a polynomial can comprise several variables. All of the same rules employ when working with polynomials containing several variables. Consider an example:

$\begin{array}{cc}\left(a+2b\right)\left(4a-b-c\right)\hfill & \hfill \\ a\left(4a-b-c\right)+2b\left(4a-b-c\right)\hfill & \phantom{\rule{2em}{0ex}}\text{Use the distributive property}.\hfill \\ 4{a}^{2}-ab-ac+8ab-2{b}^{2}-2bc\hfill & \phantom{\rule{2em}{0ex}}\text{Multiply}.\hfill \\ 4{a}^{2}+\left(-ab+8ab\right)-ac-2{b}^{2}-2bc\hfill & \phantom{\rule{2em}{0ex}}\text{Combine like terms}.\hfill \\ 4{a}^{2}+7ab-ac-2bc-2{b}^{2}\hfill & \phantom{\rule{2em}{0ex}}\text{Simplify}.\hfill \end{array}$

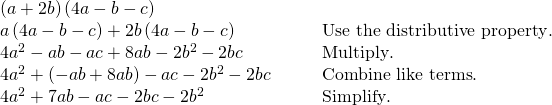
Multiplying Polynomials Containing Several Variables

Multiply $\,\left(x+4\right)\left(3x-2y+5\right).$

[reveal-respond q="fs-id1167339299948″]Prove Solution[/reveal-respond]
[hidden-answer a="fs-id1167339299948″]

Follow the same steps that we used to multiply polynomials containing just one variable.

$\begin{array}{cc}x\left(3x-2y+5\right)+4\left(3x-2y+5\right) \hfill & \phantom{\rule{2em}{0ex}}\text{Use the distributive property}.\hfill \\ 3{x}^{2}-2xy+5x+12x-8y+20\hfill & \phantom{\rule{2em}{0ex}}\text{Multiply}.\hfill \\ 3{x}^{2}-2xy+\left(5x+12x\right)-8y+20\hfill & \phantom{\rule{2em}{0ex}}\text{Combine like terms}.\hfill \\ 3{x}^{2}-2xy+17x-8y+20 \hfill & \phantom{\rule{2em}{0ex}}\text{Simplify}.\hfill \end{array}$ [/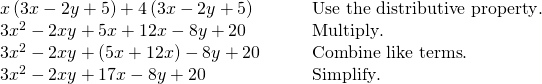subconscious-answer]

Try It

Multiply $\left(3x-1\right)\left(2x+7y-9\right).$

[reveal-answer q="fs-id1167339240262″]Show Solution[/reveal-reply]
[hidden-answer a="fs-id1167339240262″]

$\,6{x}^{2}+21xy-29x-7y+9$

[/hidden-answer]

Key Concepts

A polynomial is a sum of terms each consisting of a variable raised to a non-negative integer power. The degree is the highest power of the variable that occurs in the polynomial. The leading term is the term containing the highest degree, and the leading coefficient is the coefficient of that term. Meet (Figure).
We tin add together and decrease polynomials by combining like terms. Meet (Figure) and (Figure).
To multiply polynomials, utilize the distributive property to multiply each term in the first polynomial by each term in the second. And so add the products. Encounter (Figure).
FOIL (Get-go, Outer, Inner, Concluding) is a shortcut that tin be used to multiply binomials. See (Figure).
Perfect square trinomials and divergence of squares are special products. Meet (Figure) and (Figure).
Follow the same rules to piece of work with polynomials containing several variables. See (Effigy).

Section Exercises

Exact

Evaluate the following argument: The degree of a polynomial in standard form is the exponent of the leading term. Explicate why the statement is true or false.

[reveal-answer q="fs-id1167339216132″]Show Solution[/reveal-reply]
[hidden-reply a="fs-id1167339216132″]

The statement is true. In standard form, the polynomial with the highest value exponent is placed first and is the leading term. The caste of a polynomial is the value of the highest exponent, which in standard form is also the exponent of the leading term.

[/hidden-answer]

Many times, multiplying two binomials with two variables results in a trinomial. This is not the example when there is a difference of two squares. Explain why the product in this instance is too a binomial.

You can multiply polynomials with any number of terms and any number of variables using four basic steps over and over until yous reach the expanded polynomial. What are the four steps?

[reveal-answer q="fs-id1167339216153″]Show Solution[/reveal-reply]
[subconscious-answer a="fs-id1167339216153″]

Apply the distributive belongings, multiply, combine like terms, and simplify.

[/hidden-respond]

State whether the post-obit statement is truthful and explicate why or why not: A trinomial is always a higher degree than a monomial.

Algebraic

For the post-obit exercises, identify the degree of the polynomial.

$7x-2{x}^{2}+13$

[reveal-answer q="fs-id1167339299770″]Show Solution[/reveal-answer]
[hidden-respond a="fs-id1167339299770″]

[/hidden-answer]

$14{m}^{3}+{m}^{2}-16m+8$

$-625{a}^{8}+16{b}^{4}$

[reveal-answer q="fs-id1167339268841″]Show Solution[/reveal-answer]
[hidden-answer a="fs-id1167339268841″]

[/subconscious-answer]

$200p-30{p}^{2}m+40{m}^{3}$

${x}^{2}+4x+4$

[reveal-respond q="fs-id1167339223177″]Show Solution[/reveal-answer]
[subconscious-answer a="fs-id1167339223177″]

[/hidden-answer]

$6{y}^{4}-{y}^{5}+3y-4$

For the following exercises, find the sum or difference.

$\left(12{x}^{2}+3x\right)-\left(8{x}^{2}-19\right)$

[reveal-answer q="fs-id1167339432656″]Bear witness Solution[/reveal-reply]
[subconscious-answer a="fs-id1167339432656″]

$4{x}^{2}+3x+19$

[/hidden-reply]

$\left(4{z}^{3}+8{z}^{2}-z\right)+\left(-2{z}^{2}+z+6\right)$

$\left(6{w}^{2}+24w+24\right)-\left(3w{}^{2}-6w+3\right)$

[reveal-answer q="fs-id1167339223800″]Show Solution[/reveal-answer]
[subconscious-respond a="fs-id1167339223800″]

$3{w}^{2}+30w+21$

[/hidden-answer]

$\left(7{a}^{3}+6{a}^{2}-4a-13\right)+\left(-3{a}^{3}-4{a}^{2}+6a+17\right)$

$\left(11{b}^{4}-6{b}^{3}+18{b}^{2}-4b+8\right)-\left(3{b}^{3}+6{b}^{2}+3b\right)$

[reveal-answer q="fs-id1167339273678″]Evidence Solution[/reveal-respond]
[hidden-answer a="fs-id1167339273678″]

$11{b}^{4}-9{b}^{3}+12{b}^{2}-7b+8$

[/subconscious-reply]

$\left(49{p}^{2}-25\right)+\left(16{p}^{4}-32{p}^{2}+16\right)$

For the following exercises, find the product.

$\left(4x+2\right)\left(6x-4\right)$

[reveal-answer q="fs-id1167339259665″]Bear witness Solution[/reveal-respond]
[hidden-answer a="fs-id1167339259665″]

$24{x}^{2}-4x-8$

[/hidden-answer]

$\left(14{c}^{2}+4c\right)\left(2{c}^{2}-3c\right)$

$\left(6{b}^{2}-6\right)\left(4{b}^{2}-4\right)$

[reveal-reply q="fs-id1167339223456″]Bear witness Solution[/reveal-answer]
[hidden-reply a="fs-id1167339223456″]

$24{b}^{4}-48{b}^{2}+24$

[/hidden-reply]

$\left(3d-5\right)\left(2d+9\right)$

$\left(9v-11\right)\left(11v-9\right)$

[reveal-answer q="fs-id1167339306603″]Evidence Solution[/reveal-answer]
[hidden-answer a="fs-id1167339306603″]

$99{v}^{2}-202v+99$

[/subconscious-respond]

$\left(4{t}^{2}+7t\right)\left(-3{t}^{2}+4\right)$

$\left(8n-4\right)\left({n}^{2}+9\right)$

[reveal-answer q="fs-id1167339286568″]Show Solution[/reveal-answer]
[hidden-answer a="fs-id1167339286568″]

$8{n}^{3}-4{n}^{2}+72n-36$

[/hidden-respond]

For the post-obit exercises, expand the binomial.

${\left(4x+5\right)}^{2}$

${\left(3y-7\right)}^{2}$

[reveal-answer q="fs-id1167339199549″]Testify Solution[/reveal-answer]
[hidden-answer a="fs-id1167339199549″]

$9{y}^{2}-42y+49$

[/hidden-answer]

${\left(12-4x\right)}^{2}$

${\left(4p+9\right)}^{2}$

[reveal-answer q="fs-id1167339220312″]Show Solution[/reveal-reply]
[hidden-answer a="fs-id1167339220312″]

$16{p}^{2}+72p+81$

[/hidden-reply]

${\left(2m-3\right)}^{2}$

${\left(3y-6\right)}^{2}$

[reveal-reply q="fs-id1167339226366″]Show Solution[/reveal-answer]
[hidden-answer a="fs-id1167339226366″]

$9{y}^{2}-36y+36$

[/subconscious-reply]

${\left(9b+1\right)}^{2}$

For the post-obit exercises, multiply the binomials.

$\left(4c+1\right)\left(4c-1\right)$

[reveal-reply q="fs-id1167339196498″]Show Solution[/reveal-reply]
[hidden-answer a="fs-id1167339196498″]

$16{c}^{2}-1$

[/hidden-answer]

$\left(9a-4\right)\left(9a+4\right)$

$\left(15n-6\right)\left(15n+6\right)$

[reveal-answer q="fs-id1167339260447″]Bear witness Solution[/reveal-answer]
[subconscious-answer a="fs-id1167339260447″]

$225{n}^{2}-36$

[/hidden-reply]

$\left(25b+2\right)\left(25b-2\right)$

$\left(4+4m\right)\left(4-4m\right)$

[reveal-answer q="fs-id1167339239040″]Testify Solution[/reveal-answer]
[hidden-answer a="fs-id1167339239040″]

$-16{m}^{2}+16$

[/subconscious-answer]

$\left(14p+7\right)\left(14p-7\right)$

$\left(11q-10\right)\left(11q+10\right)$

[reveal-respond q="fs-id1167339239169″]Prove Solution[/reveal-reply]
[hidden-answer a="fs-id1167339239169″]

$121{q}^{2}-100$

[/hidden-answer]

For the following exercises, multiply the polynomials.

$\left(2{x}^{2}+2x+1\right)\left(4x-1\right)$

$\left(4{t}^{2}+t-7\right)\left(4{t}^{2}-1\right)$

[reveal-answer q="fs-id1167339138777″]Show Solution[/reveal-answer]
[hidden-answer a="fs-id1167339138777″]

$16{t}^{4}+4{t}^{3}-32{t}^{2}-t+7$

[/hidden-answer]

$\left(x-1\right)\left({x}^{2}-2x+1\right)$

$\left(y-2\right)\left({y}^{2}-4y-9\right)$

[reveal-answer q="fs-id1167339273787″]Prove Solution[/reveal-answer]
[subconscious-reply a="fs-id1167339273787″]

${y}^{3}-6{y}^{2}-y+18$

[/hidden-answer]

$\left(6k-5\right)\left(6{k}^{2}+5k-1\right)$

$\left(3{p}^{2}+2p-10\right)\left(p-1\right)$

[reveal-answer q="fs-id1167339344407″]Bear witness Solution[/reveal-answer]
[hidden-reply a="fs-id1167339344407″]

$3{p}^{3}-{p}^{2}-12p+10$

[/hidden-respond]

$\left(4m-13\right)\left(2{m}^{2}-7m+9\right)$

$\left(a+b\right)\left(a-b\right)$

[reveal-answer q="fs-id1167339344562″]Evidence Solution[/reveal-answer]
[hidden-reply a="fs-id1167339344562″]

${a}^{2}-{b}^{2}$

[/hidden-reply]

$\left(4x-6y\right)\left(6x-4y\right)$

${\left(4t-5u\right)}^{2}$

[reveal-answer q="fs-id1167339214045″]Show Solution[/reveal-respond]
[hidden-answer a="fs-id1167339214045″]

$16{t}^{2}-40tu+25{u}^{2}$

[/hidden-reply]

$\left(9m+4n-1\right)\left(2m+8\right)$

$\left(4t-x\right)\left(t-x+1\right)$

[reveal-answer q="fs-id1167339222924″]Show Solution[/reveal-answer]
[hidden-answer a="fs-id1167339222924″]

$4{t}^{2}+{x}^{2}+4t-5tx-x$

[/subconscious-respond]

$\left({b}^{2}-1\right)\left({a}^{2}+2ab+{b}^{2}\right)$

$\left(4r-d\right)\left(6r+7d\right)$

[reveal-answer q="fs-id1167339225614″]Show Solution[/reveal-respond]
[hidden-reply a="fs-id1167339225614″]

$24{r}^{2}+22rd-7{d}^{2}$

[/subconscious-respond]

$\left(x+y\right)\left({x}^{2}-xy+{y}^{2}\right)$

Real-Globe Applications

A developer wants to buy a plot of country to build a house. The expanse of the plot can be described by the post-obit expression: $\,\left(4x+1\right)\left(8x-3\right)\,$ where x is measured in meters. Multiply the binomials to find the area of the plot in standard form.

[reveal-answer q="fs-id1167339225791″]Show Solution[/reveal-answer]
[subconscious-answer a="fs-id1167339225791″]

$32{x}^{2}-4x-3\,$ m²

[/hidden-answer]

A prospective heir-apparent wants to know how much grain a specific silo tin hold. The area of the flooring of the silo is $\,{\left(2x+9\right)}^{2}.\,$ The superlative of the silo is $\,10x+10,$ where x is measured in feet. Expand the square and multiply by the height to find the expression that shows how much grain the silo can concur.

Extensions

For the post-obit exercises, perform the given operations.

${\left(4t-7\right)}^{2}\left(2t+1\right)-\left(4{t}^{2}+2t+11\right)$

[reveal-reply q="fs-id1167339243163″]Prove Solution[/reveal-answer]
[subconscious-answer a="fs-id1167339243163″]

$32{t}^{3}-100{t}^{2}+40t+38$

[/subconscious-respond]

$\left(3b+6\right)\left(3b-6\right)\left(9{b}^{2}-36\right)$

$\left({a}^{2}+4ac+4{c}^{2}\right)\left({a}^{2}-4{c}^{2}\right)$

[reveal-answer q="fs-id1167339230976″]Show Solution[/reveal-answer]
[hidden-answer a="fs-id1167339230976″]

${a}^{4}+4{a}^{3}c-16a{c}^{3}-16{c}^{4}$

[/hidden-answer]

diazladvized.blogspot.com

Source: https://opentextbc.ca/algebratrigonometryopenstax/chapter/polynomials/

Mid-unit Review Multiply Using Foil or by the Front Term

Polynomials

Learning Objectives

Identifying the Degree and Leading Coefficient of Polynomials

Polynomials

How To

Attempt Information technology

Adding and Subtracting Polynomials

How To

Adding Polynomials

Analysis

Try Information technology

Subtracting Polynomials

Analysis

Effort It

Multiplying Polynomials

Multiplying Polynomials Using the Distributive Belongings

How To

Multiplying Polynomials Using the Distributive Property

Endeavor It

Using FOIL to Multiply Binomials

How To

Using FOIL to Multiply Binomials

Try It

Perfect Square Trinomials

Perfect Square Trinomials

How To

Expanding Perfect Squares

Try It

Difference of Squares

Difference of Squares

How To

Multiplying Binomials Resulting in a Divergence of Squares

Endeavor Information technology

Performing Operations with Polynomials of Several Variables

Multiplying Polynomials Containing Several Variables

Try It

Key Concepts

Section Exercises

Exact

Algebraic

Real-Globe Applications

Extensions

0 Response to "Mid-unit Review Multiply Using Foil or by the Front Term"

Post a Comment

Iklan Atas Artikel

Iklan Tengah Artikel 1

Iklan Tengah Artikel 2

Iklan Bawah Artikel